一. 由数学危机到图灵机
1.1 历史上的三次数学危机
1.2 第一次 - 无理数
毕达哥拉斯学派(公元前500年)
- 信仰数是万物本源
- 信仰一切皆可表成整数或者整数之比
直到
- 毕达哥拉斯证明了勾股定理,同时发现三角形某些边不能通过整数标识
- 西帕索斯悖论,边长为一的正方形,对角线是多少。
缓解
- 欧多克索斯通过几何方法建立比例论,避开了无理数的产生
解决
- 十九世纪下半叶,实数理论的建立,确立无理数在数学中的合法地位
1.3 第二次 - 微积分
- 十七世纪牛顿和莱布尼兹各自独立发现了微积分,但两人的理论都建立在无限小分析之上
- 贝克莱悖论,嘲笑微积分
缓解
十九世纪七十年代,实数理论的建立
1.4 第三次 - 集合论
- 十九世纪康托尔创立集合论,声称自然数和集合论一起可以重建整个数学大厦
直到
- 罗素悖论
- 一个理发师只给所有不给自己理发的人理发,不给那些给自己理发的人理发,问:他要不要自己理发?(答案:要,他给自己理发,和前半句冲突。 不要,他不给自己理发,和后半句冲突
- S由一切不属于自身元素的集合组成,S是否属于S。
缓解
哥德尔,1931年成功证明:任何一个数学系统,只要它是从有限的公理和基本概念中推到出来的, 并且能从中推证出自然数系统,就可以在其中找到一个命题 ,就可以在其中找到一个命题, 对于它, 我们既无法证真,也无法证伪。
这里就是对应上面的罗素悖论,通过公理和基本概念推到出来的集合论里面,罗素悖论这个命题无法证真也无法证伪。
这个定理称为,哥德尔不完备性定理
- 这个定理宣告了把数学彻底形式化的愿望不可实现
解决第三次危机后,接下来的问题
在一个系统中,有的问题可以证真也可以证伪,但是有些问题既不能证真也不能证伪,如何判定一个问题是否能被证真或者证伪。
在计算机中把这个问题,称为可计算问题:
- 假设函数f定义域为D,值域为R,如果存在一种算法,对D中任意给定的x,都能计算出f(x)的值,则称f函数是可计算的。
研究思路:
为计算建立一种数学模型,称之为计算模型。然后证明,凡是这个计算模型能够完成的任务称之为可计算任务。
二. 图灵机
图灵提出来这么一个模型-图灵机
- 1936年,发表了著名论文《论可计算数在判定问题中的应用》,在文中提出了一种理想的计算机器的数学模型-图灵记。
2.1 图灵机组成
- 一条存储带
- 带子可以两边无限延长
- 带子上均匀分布一个个的小方格
- 每个小方格可以存储一个字符
- 一个控制器
- 一个读写头,可以读写,更改带子上的每一格字符
- 可以接受设定好的程序
- 可以储存当前的自身状态
- 可以变换自身的状态
- 可以沿着存储带左右移动
2.2 图灵机工作步骤
2.2.1 准备
- 存储带上的符号初始化
- 设定好控制器自身状态
- 控制器置于起始位置
- 准备好工作程序
2.2.2 反复执行下一步骤直到停机
- 读出存储带字符
- 根据自身状态和读出的字符,找到相应的程序语句
- 根据程序语句,做三个动作:
- 在当前格子内写入一个字符
- 更新自身状态
- 读写头向左或者向右移动一格
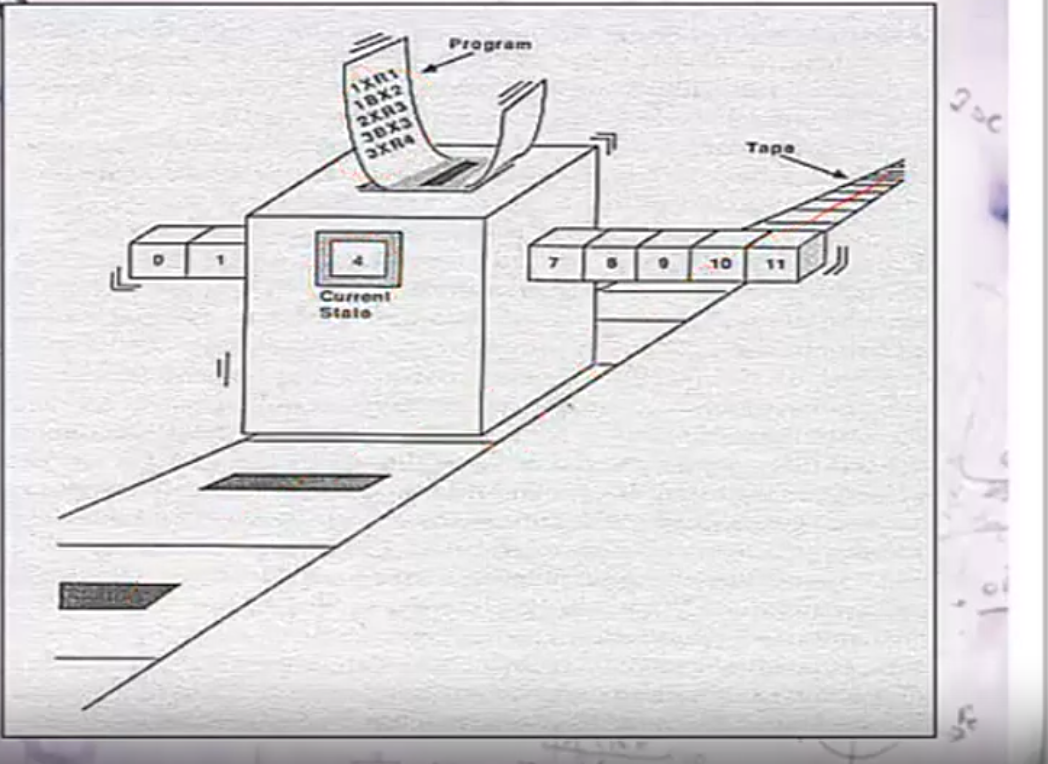
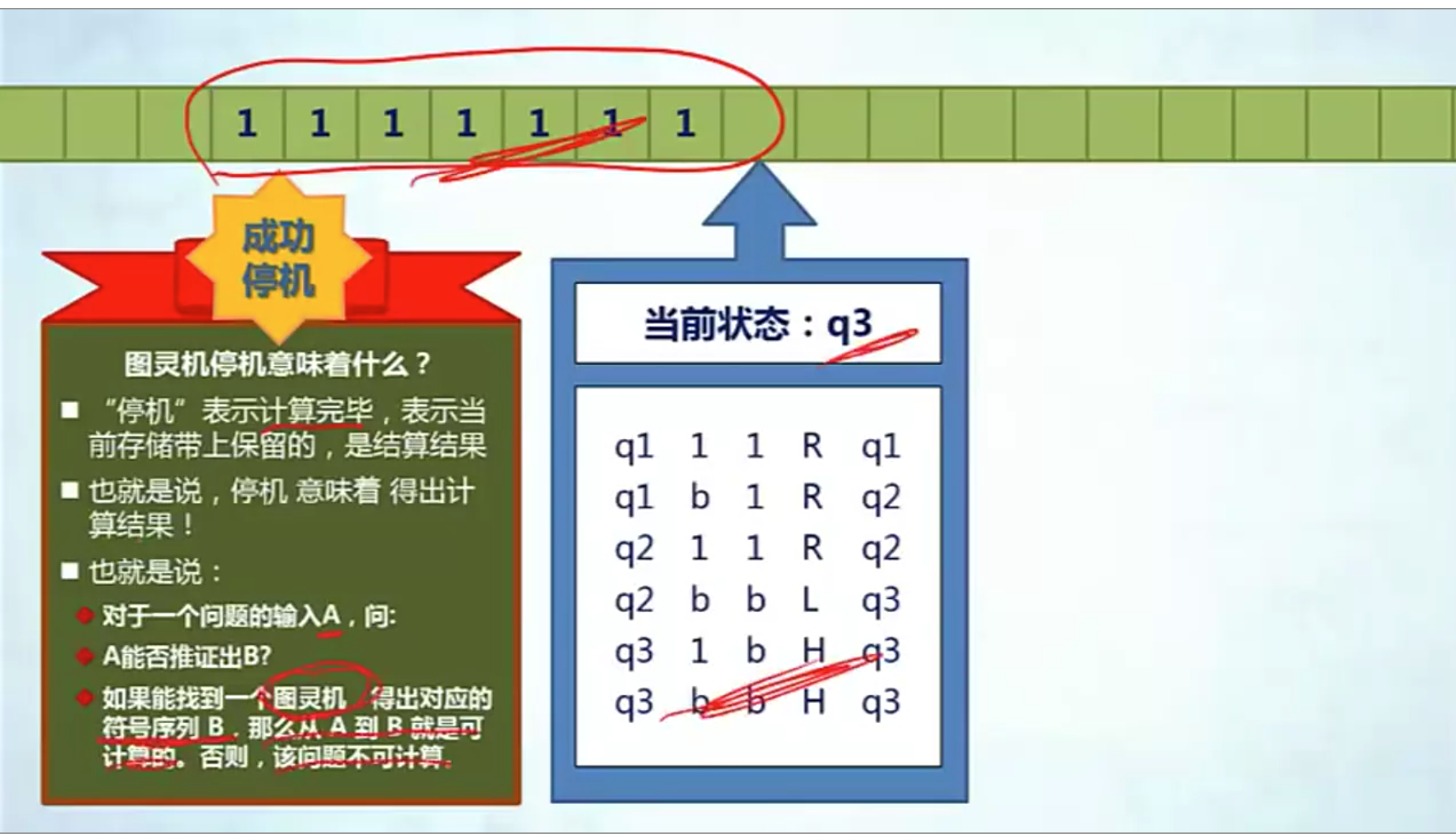
上面展示的就是以二进制作为字母表,下面的框框就是程序,程序中每一列含义
第一列:当前状态
第二列:读出来的字符
第三列:写进去的字符
第四列:左移还是右移
第五列:更新的状态
三. 计算机为什么能计算?
要回答这个问题,可以把这个拆分成三个子问题:
- 数 在计算机中是如何表示的?
- 逻辑上的 数 是如何计算的?
- 物理上的 数 的计算是如何实现的?
3.1 为什么计算机采用的是二进制?
关于计算机的数如何表示的
- 采用字母表,像图灵记那样子,1表示1,b表示边界
- 问题:数值 10000 ,需要用一万个字母1表示,读入这一个数,需要读写头移动一万次,不合理
- 优化:采用十进制作为字母表,字母表包含{1,2,3…,9,b},计算2001+1999,每一位都有一个字母表示,
- 问题,虽然移动次数变少了,但是程序的控制量变大了,确定当前指令也需要更多的时间
二进制字母表程序 与 十进制字母表程序 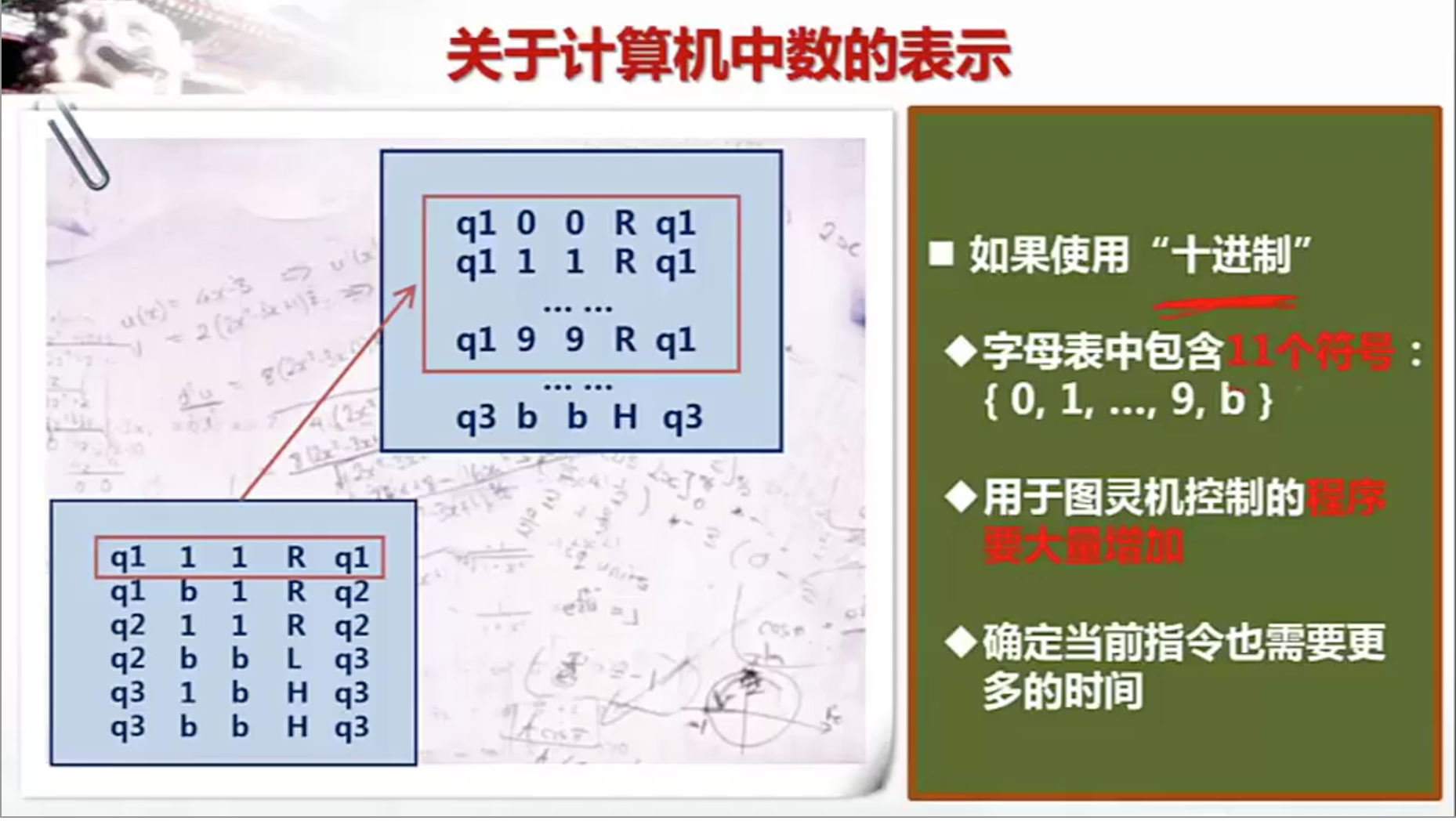
``
由上可知
- 字符表的符号越多,移动的次数变少了(1万个1表示一万,和五个十进制字符表示10000),但是程序量变大,确定程序语句时搜索空间变大了
- 字符表的符号越少,移动的次数变多,程序量变小
那么这个字符表太多了不行,太少了也不行,那么进过研究,最后提出来的是:
- 字符表的最优数量,可能是欧拉常数e,2.71828…..,取整数后就为3.
- 与具有两个状态的电子元件相比,具有三个状态的电子元器件在制造上更加困难,可靠性低(二极管,三极管)
回答开始提出的问题,为什么计算机采用的是二进制:
两个字符的字符表相对来说更加便捷,在磁带移动与程序的寻址空间中的一个折中选择,并且更加符合我们的工艺水平(二极管可靠,制造成本低)
3.2 数的表示
十进制
- 计数符号:0,1,2,3,4,5,6,7,8,9
- 数的表示:$256=2\times10^2+5\times10^1+5\times10^0$
二进制
- 计数符号:0,1
- 数的表示:$10110=1\times2^4+0\times2^3+1\times2^2+1\times2^1+0\times2^0$
十六进制
- 计数符号:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
- 数的表示:$(ABCD)_{16}=A\times16^3+B\times16^2+C\times16^1+D\times16^0$
其他进制转10进制:$符号\times基数^位$
十进制转二进制:整数除以2的商的余数
123/2=61…..1
61/2=30……1
20/2=15……0
15/2=7……..1
7/2=3……..1
3/2=1…..1
1/2=0…..1
自下往上,1111011
拓展:
其他进制如何直接转成2进制
从左往右,将每个进制字符当成一个十进制值,每个字符除以2取余数直到商为0,获取当前字符的二进制,最后拼接起来
$(AB)_{16}$转换成二进制
A/2=5….0 B/2=5…..1
5/2=2….1 5/2=2……1
2/2=1….0 2/2=1……0
1/2=0….1 1/2=0……1
1010 1011
二进制如何直接转成其他进制
以2为底,求对数 $log_2{进制}$,值代表多少个二进制位能代表一个此进制符号。
从右往左,固定个二进制位转换成一个对应进制符号,拼接起来便是
$1011101{(2)}=(001 011 101){(2)}=135_{(8)}$
$1011101{(2)}=0101 1101 _{(2)}=5D{(16)}$
3.3 计算机如何进行计算
3.3.1 布尔代数
- 1854年,布尔发表了《思维规律的研究-逻辑与概率的数学理论基础》,并综合其另一篇文章《逻辑的数学分析》,创立了一门全新的学科 - 布尔代数
- 为计算机开关电路的设计提供了重要的数学方法和理论基础。(与或非门)
- 基本逻辑运算
- 与
- 或
- 非
- 复合逻辑运算
- 同或 异或
- 与非
- 或非
- 与或非
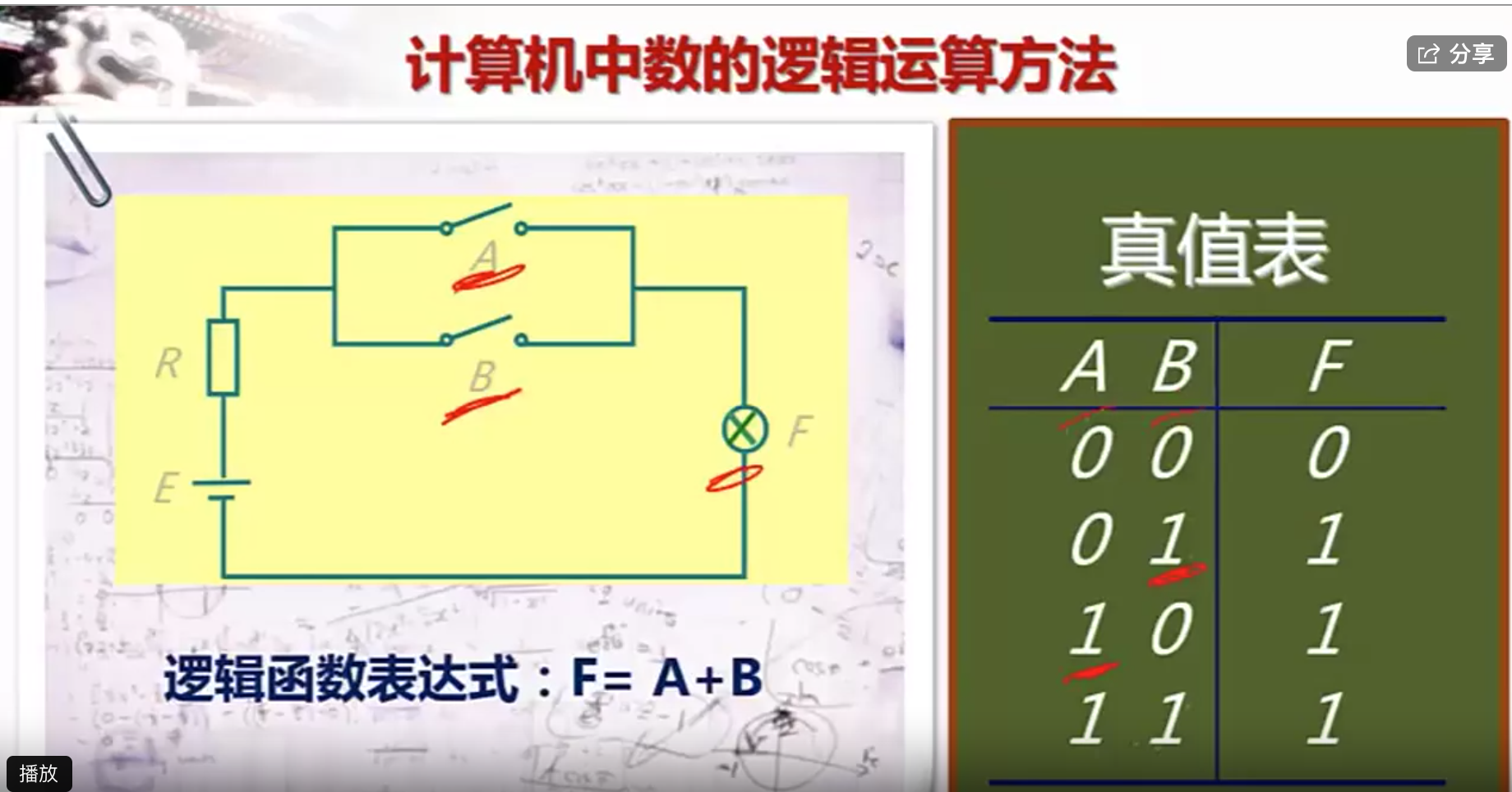
把A B当成两个变量,F为运算结果,1表示闭合,0表示开启,f中的0表示灭,1表示亮。
以电路是否通,灯是否量的这种规律来表示逻辑运算
与运算 $F=a\cdot b$
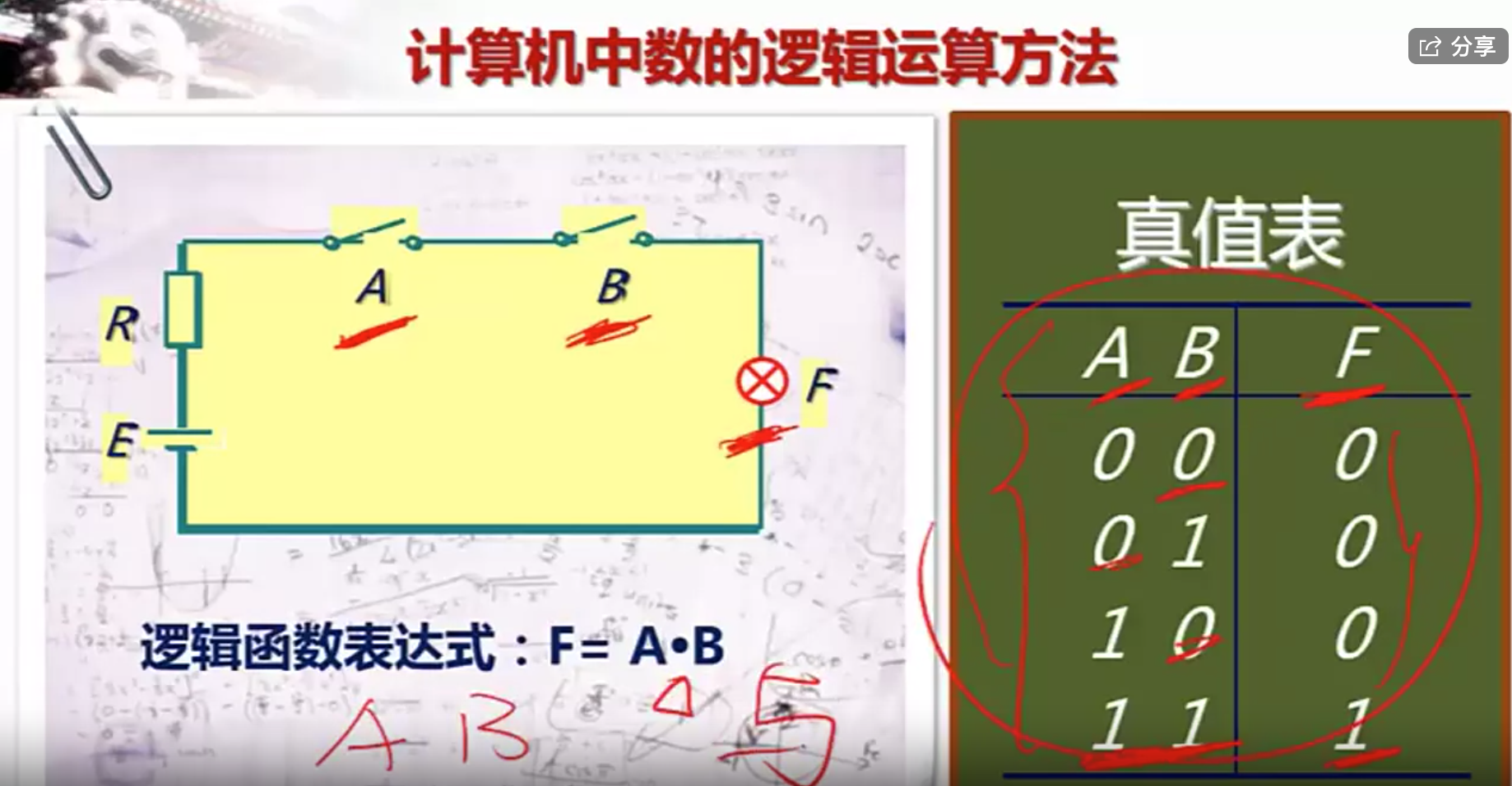
或运算$F=A+B$
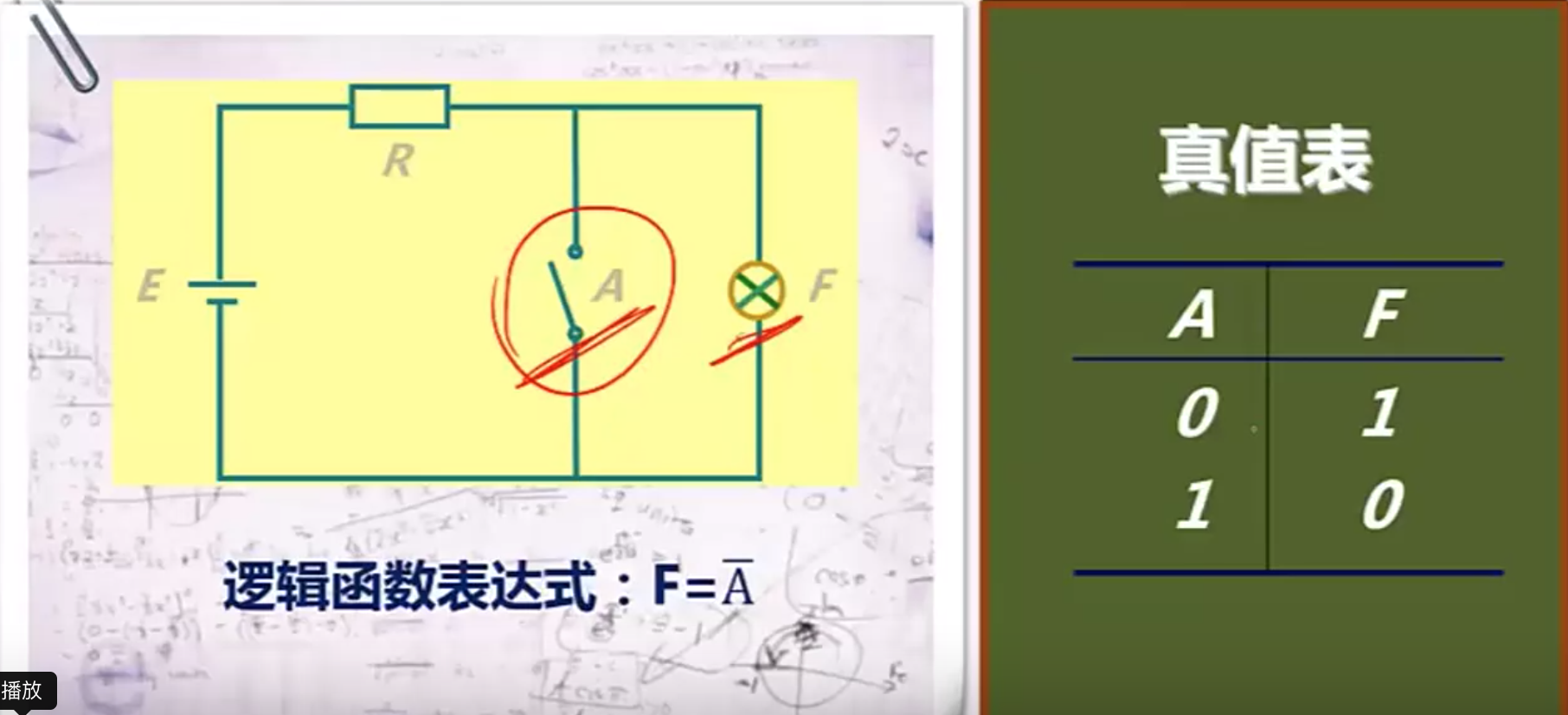
非运算F=A
复合运算

如何做加法运算

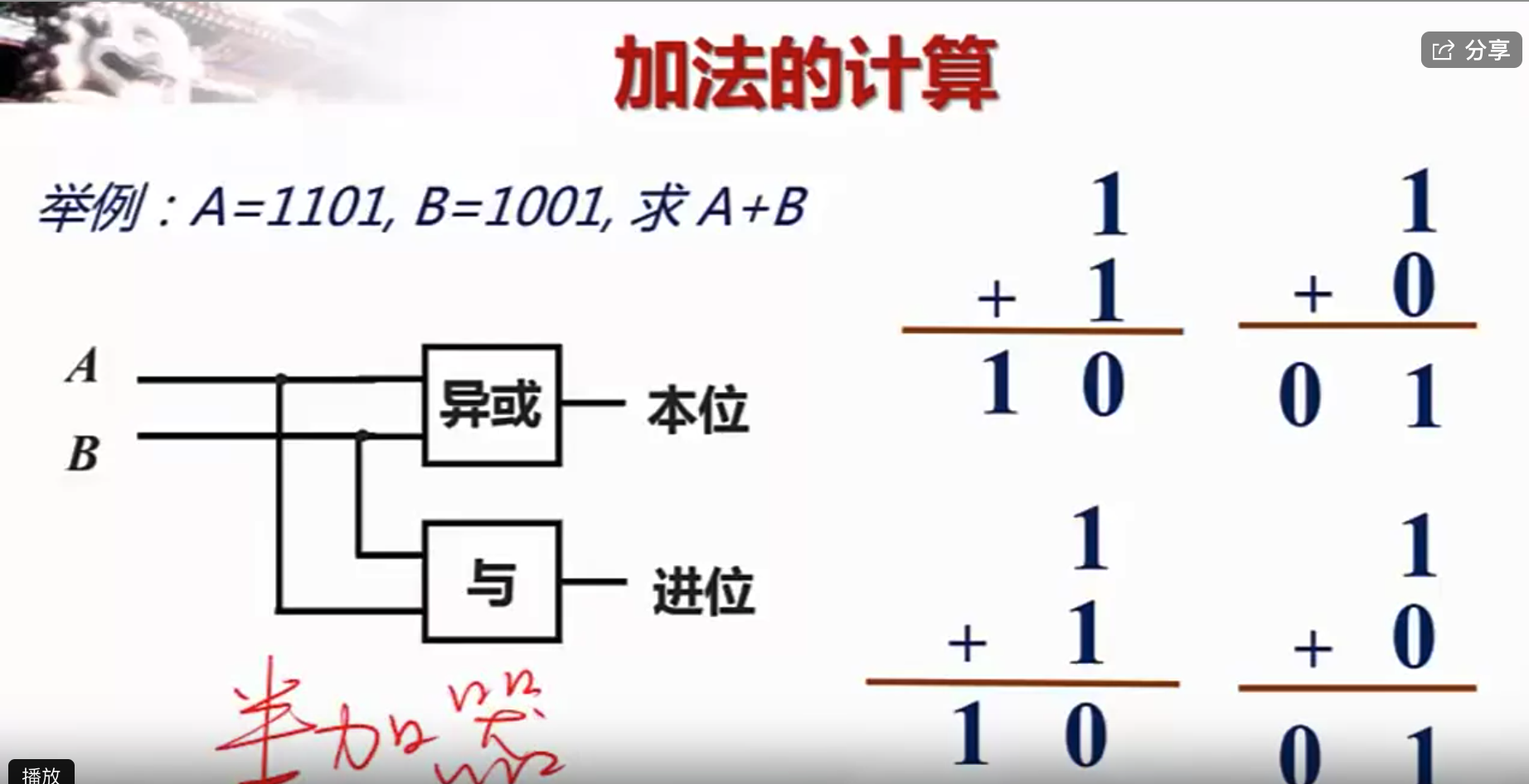
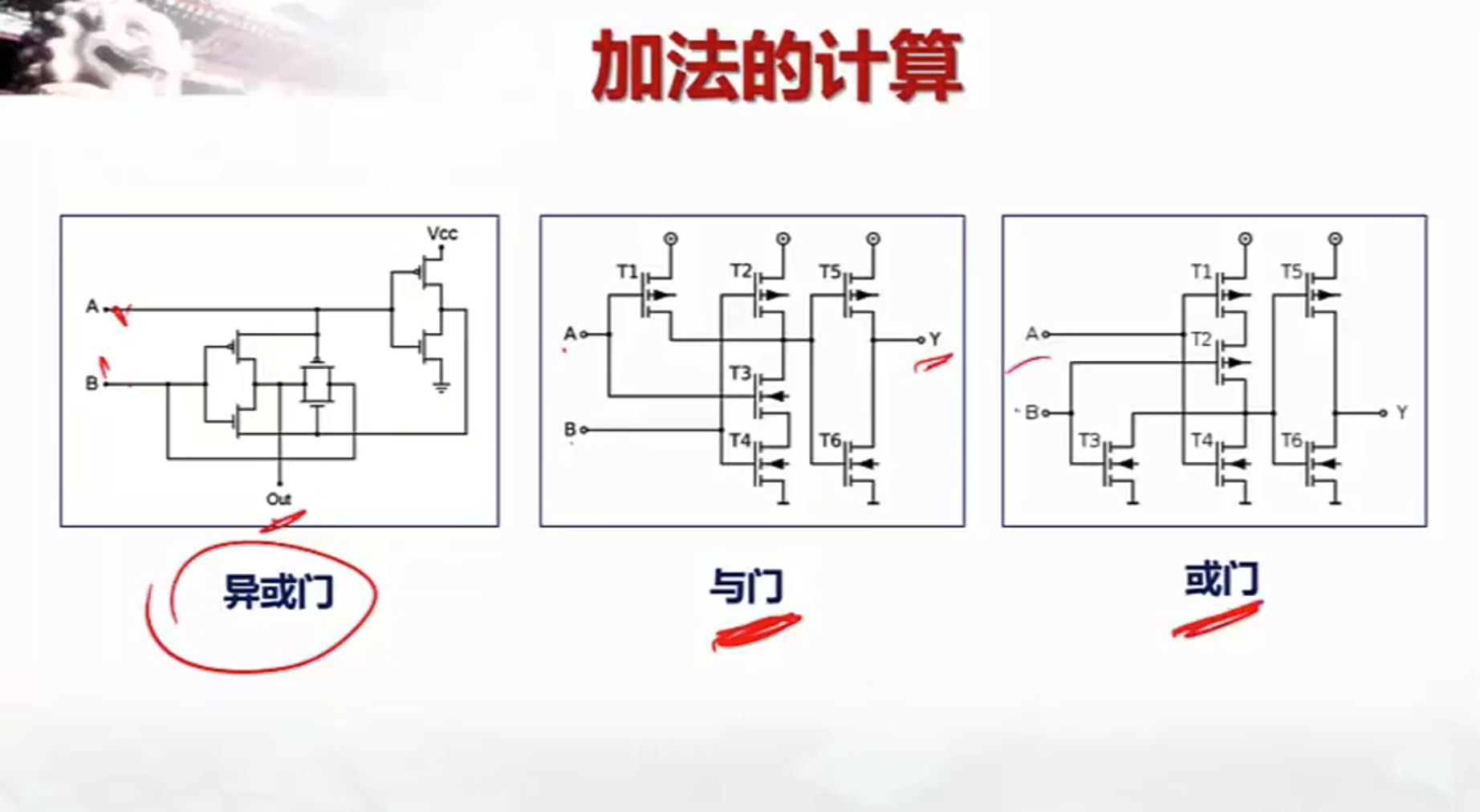
小结
- 参与运算的数能够转换成二进制
- 二进制数的运算可以通过基本的“布尔运算”实现
- 基本的“布尔运算”都可以通过电路实现
结论:电路能算数!
附录